2021/12/22

Interpretability/explainability in machine learning

Author:: YuhiK8

, 2021/12/22

Interpretability/explainability in machine learning

* This article is a translation of the Japanese article written on Dec. 24th, 2019.

Hello! On day 24 of the Merpay Advent Calendar 2019, I (@yuhi) from the Merpay Machine Learning team will share interpretability in machine learning.

What is interpretability in machine learning?
Why do we need interpretability?
What approaches are available?
About SHAP
About implementing SHAP
Conclusion
References

What is Interpretability in machine learning?

With the development of machine learning, including deep learning, unique services that have never been seen before are being developed, and business operations in many industries are becoming more efficient and sophisticated. For example, at Merpay, we use machine learning to build credit scoring models and fraud detection services.

However, as machine learning is generally referred to as a “black box,” it is often difficult to understand why we get a particular result using a model having a complex hypothesis space. For this reason, there has been a lot of research on making the learning done and inference results produced by a machine learning model easily interpretable by humans [1] .

There seems to be no clear definition of Interpretability, but I quote the following [2]；

the degree to which
an observer can understand the cause of a decision.

Here, Interpretability is defined as the degree to which an observer can understand the factors of a decision (made by a model). It is desirable to have a high degree of Interpretability, such that humans can easily understand the inference results from the trained model.

Why do we need interpretability?

For example, here are some of the reasons why high interpretability is necessary:

Accountability as a business operator providing services
Understanding of inference results among stakehokders inside and outside the company
Debugging and accuracy improvement of model

1. Accountability as a business operator providing services

Not all machine learning systems will be held accountable. It depends on the domain where machine learning will be applied. According to the draft AI development guidelines developed by the Ministry of Internal Affairs and Communications [3]；

②Principle of transparency——-
Developers should pay attention to the verifiability of inputs/outputs and the accountability of decision results of AI systems. AI systems subject to this principle are assumed to be those that may affect the life, bodily integrity, freedom, privacy, property, etc., of users and third person.
(translated by author of this article)

In areas where the inferences of machine learning models can have serious consequences, such as health care, finance, and automated driving, it isn’t hard to imagine that prediction accuracy and interpretability are required. Instead, interpretable models are often used, even at the expense of performance.

2. Understanding of inference results among stakeholders inside and outside the company

In many cases, it isn’t easy to convince people of the prediction results only by explaining the evaluation metrics (e.g., RMSE, AUC), especially if you are in charge of product development or modeling as a data scientist or machine learning engineer. There are many possible reasons for this. According to one theory [4], it is related to our fundamental human nature, such as curiosity about unexpected events and searching for meaning in events that happened.

In fact, and this is true in my experience, I believe that answering stakeholders’ "why" to learning and inference results will help them feel satisfied and help us move the business forward as a team.

3. Debugging and accuracy improvement of model

From a developer’s perspective, debugging and improving predictive performance of the mode is very important. These two elements strongly support data scientists and machine learning engineers in a series of processes, such as checking whether explanatory variables that may lead to leakage are used, selecting explanatory variables, and analyzing errors to improve accuracy, which provide information for deciding the following action.

What approaches are available?

So what are some of the approaches to providing interpretability? There seem to be various ways to classify them [5]. Here I will refer to an article [1].

Approaches that give a broad explanation; we want to know which features are essential or dominant.
- GLM (Generalized Linear Regression Model)
- Decision tree
- Feature Importance
- Partial Dependence
- Sensitivity analysis, etc.
Approaches that give local explanations; we want to know how each feature value contributes to the prediction for a given input.
- LIME (Local Interpretable Model – agnostic Explanations) [6]
- SHAP (SHapley Additive exPlanations) [7]　etc.

I want to introduce SHAP in this post, although some of you may already know about it. As to other approaches, please refer to the easy-to-grasp information available here [1][8].

SHAP

I will now focus on a paper of SHAP [7].

I will write about the details of SHAP below. If you are interested in the usability of SHAP as a tool, please go down to “About implementation of SHAP”.

Summary

Methods for giving post hoc explanations such as LIME, DeepLIFT, and Layer-Wise Relevance Propagation can be generalized as Additive Feature Attribution Methods.
- It calculates the contribution by building an explainable approximate model for a given data point.
Additive Feature Attribution Methods are synonymous with Shapley values used in cooperative game theory.
Shapley values are expected values of each player’s degree of contribution in a cooperative game. Each player corresponds to a feature value (reflecting that the Shapley value represents each feature value’s degree of contribution).

Basic ideas

In the Additive Feature Attribution Methods, we find a function \(g\) that approximates the function \(f\) obtained from learning for a given data point. For \(g\), we choose an interpretable hypothesis space such as a linear model or a decision tree to make it possible to interpret the prediction results for a given data point.

Problem setting

Let the input space be \(\mathcal X\), and the original hypothesis space be \(\mathcal H\). For \(\mathcal H\), the user can freely specify any model such as Gradient Boosting Decision Tree, Support Vector Machine, or Neural Network. For all data point \(x \in \mathcal X\), we find a function \(g \in \mathcal G\) that approximates the function
\(f\in \mathcal H\) (hereafter, we call this an explainable model). Let \(x' \in \{0,1\}^M\) denote the simplified data point of the data point of interest \(x \in \mathcal X\).
In the space of simplified data points, 0 corresponds to "feature value does not exist," and 1 corresponds to "feature value exists."
The explainable model is a set of hypotheses such as;

\(\displaystyle{\mathcal G := \Big\{g:z' \to \phi_0 + \sum_{i=1}^{M}\phi_iz'_i \mid z' \in \{0,1\}^M,\,\phi_0 \in \mathbb R, \phi_i \in \mathbb R\Big\}}\)

And we find a function \(g\) in this set of hypotheses such that\(g(z') \approx f\big(h_x(z')\big)\) when \(z' \approx x'\). We further assume that we can restore the data point of interest \(x \in \mathcal X\) as \(x = h_x(x')\) by the mapping \(h_x : \{0,1\}^M \mapsto \mathcal X\).

Note that G is clearly a set of linear regression models.

Properties to be satisfied for an explainable model

If we define three properties that we want the explainable model \(\mathcal G\) to satisfy, then feature attribution of i-th element\(\phi_i\) satisfying those three properties is uniquely determined in the following format. Therefore, \(g\) is uniquely determined.

\(\displaystyle{\mathcal \phi_i(f, x ) = \sum_{z' \subseteq \ x'}\frac {|z'|!\big(M - |z'| -1\big)!} {M!} \big[f_x(z') - f_x(z_{\setminus i}')\big].}\)

Where \(|z'|\) denotes the number of nonzero elements of the vector \(z'\), \(z' \subseteq x'\) means all the elements of the subset of nonzero elements of \(x'\), \(\ f_x(z') := f_x(h_x(z')) = \mathbb E [ f(z) | z_S ]\)、\(S = \{ i \mid z'_i \neq 0 \}\).

Furthermore, this feature attribution\(\phi_i\) is known as the Shapley value in cooperative game theory, meaning the degree of contribution of the \(i\)-th element of the input.

(Local accuracy)

\(\displaystyle{f(x) = g(x')}.\)

This formula expresses expectation when \(x = h_x(x')\), that is when we use the simplified data point \(x' \in \{ 0,1 \}^M\) that corresponds to the data point of interest \(x \in \mathcal X\) as input data. Thus, we want the prediction value of the the original model \(f \in \mathcal H\) to match the the explainable model \(g\in \mathcal G\).

(Missingness)

\(\displaystyle{x'_i = 0 \implies \phi_i = 0.}\)

This property indicates that we want the feature attribution to be always zero (\(\phi_i = 0\)) whenever \(x_i'\) lacks information.
In practice, it seems that \(x_i'=0\) when \(i\)-th element of the input takes a constant value (i.e., non-informative) across the entire data set (as mentioned by the author of this paper).

(Consistency)

Quated from this paper,

Let \(\ f_x(z') = f(h_x(z'))\) and \(z_{\setminus i}'\) denote setting \(z_i' = 0\). For any two models \(f\) and \(f'\), if

\(\ f'_x(z') - f'_x(z_{\setminus i}') \geq f_x(z') - f_x(z_{\setminus i}')\)

for all inputs \(z' \in \{0,1\}^M\), then \(\phi_i(f', x) \geq \phi_i(f, x)\).

For hypothesis \(f'\) where the contribution of \(i\)-th element of the input is more significant, this formula indicates that the feature attribution (Shapley values) of that \(i\)-th element of the input should not decrease.

Calculate an explainable model

We consider the following optimization problem for single data point \(x \in \mathcal X\) (we will solve this problem for the number of data points in the test dataset).

\(\displaystyle{ \min_ {g \in \mathcal G} \ L(f,g,\pi_{x'}) + \Omega(g). }\)

where

\( \begin{aligned} \Omega(g) &= 0, \\ \pi_{x'}(z') &= \frac {(M-1)} {\tbinom{M}{|z'|}|z'|(M-|z'|)}, \\ L(f,g,\pi_{x'}) &= \sum_{z' \in Z} [f(h_x(z')) - g(z')]^2 \pi_{x'}(z') \end{aligned}\)

The optimization algorithm is based on the proposed method in LIME [6] (a more efficient sampling algorithm than LIME is presented in [7] ). Without details, we sample the data from the neighborhood of the data point \(x \in \mathcal X\) and weigh it by the kernel function \(\pi_x\) to evaluate the objective function. Suppose we define \(\Omega(g), \pi_{x'}({z'}), L(f, g, \pi_x)\) as above. In this case, we are calculating SHAP values (same as Shapley values) with LIME’s algorithm to satisfy the "desired property for the explainable model" (see [7] for the proof).

About implementation of SHAP

SHAP’s author has made a very high quality implementation available on Github. Since the Python API is now publicly available, I will use Python below without any special declaration.

https://github.com/slundberg/shap

I would like to briefly introduce what kind of tool is while doing simple modeling using an open data set.

https://www.openml.org/d/40514

The problem setting is to estimate the credit risk (the likelihood of default) of an individual. The target variable is a binary of good or bad, while the number of explanatory variables is 20, including attribute information and past credit information (the meaning of the objective variable, such as how it was labeled, was not explicitly described regarding the data set). We used the LightGBM model.
The feature values used in this model are different from those used in the credit model we are developing at Merpay. Please understand that this model is shown only to demonstrate SHAP.

import pandas as pd
import numpy as np
import io
import requests
import lightgbm as lgb
import shap
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder

# load JS visualization code to notebook
shap.initjs()

cat_cols = ['checking_status', 'credit_history', 'purpose', 'savings_status',
            'employment', 'personal_status', 'other_parties', 
            'property_magnitude','housing', 'job', 'foreign_worker',
            'own_telephone', 'other_payment_plans', 'class']

def label_encoder(df, cols):
    tmp = df.copy()
    le = LabelEncoder()
    for col in cols:
        tmp[col] = le.fit_transform(tmp[col])
    return tmp

def get_data():
    URL = "https://www.openml.org/data/get_csv/4600907/BNG(credit-g).arff"
    r = requests.get(URL)
    all_df = pd.read_csv(io.BytesIO(r.content), sep=",")
    all_df_enc = label_encoder(all_df, cat_cols)
    df = all_df_enc[:50000]
    X, y = df.drop('class', axis=1), (df['class'] == 0)*1
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
    return X_train, X_test[:1000], y_train, y_test[:1000]

X_train, X_test, y_train, y_test = get_data()

model_lgb = lgb.LGBMRegressor()
model_lgb.fit(X_train, y_train, categorical_feature=cat_cols[:-1])

Next, we calculate SHAP values. Here we use the Tree SHAP [9], an algorithm that calculates SHAP values at high speed for tree-based models. The algorithm proposed in the paper on SHAP [7] corresponds to the shap.KernelExplainer class.

# explain the model's predictions using SHAP values
# (same syntax works for LightGBM, CatBoost, scikit-learn and spark models)
explainer = shap.TreeExplainer(model_lgb)
shap_values = explainer.shap_values(X_test)

I want to introduce some of the methods provided by SHAP.

# visualize the first prediction's explanation (use matplotlib=True to avoid Javascript)
shap.force_plot(explainer.expected_value, shap_values[32,:], X_test.iloc[32])

shap1

The figure above visualizes how each feature value contributes to the predicted value for specific data to be expected. The red feature values contribute to a positive shift (in the direction of increasing credit risk), and the blue feature values contribute to a negative shift (in the direction of decreasing credit risk in this case). In this example, the actual label is 1, but the predicted credit risk is about 0.80, showing that values such as checking_status (checking account status) and credit_history (past credit information) contribute significantly to the predicted value.

explainer.expected_value + shap_values[32,:].sum() # 0.8049431508030044
model_lgb.predict(X_test)[32] # 0.8049431508030043

The first line calculates the output value of the obtained explainable model
\(g(z') = \phi_0 + \sum_{i=1}^{M}\phi_iz_i'\)

The explainer.expected_value corresponds to \(\phi_0\). The second line is the output value of the learned model. You can see that the output values are almost the same for each line.

# visualize the training set predictions
shap.force_plot(explainer.expected_value, shap_values, X_test)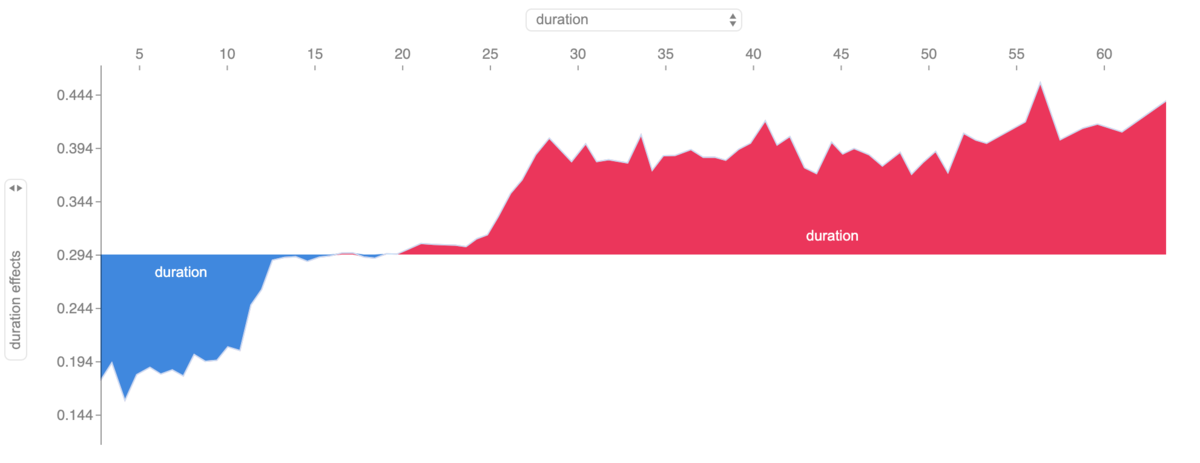

shap2

The figure above visualizes how a single feature value affects the prediction value. In addition, we can check how the predicted value changes in response to changes in the feature value. This functionality is interactive, allowing us to change the two axes at will. For example, in the above figure, we can see that people with longer due months (to the rightward of the horizontal axis) tend to have higher credit risk.

# summarize the effects of all the features
shap.summary_plot(shap_values, X_test)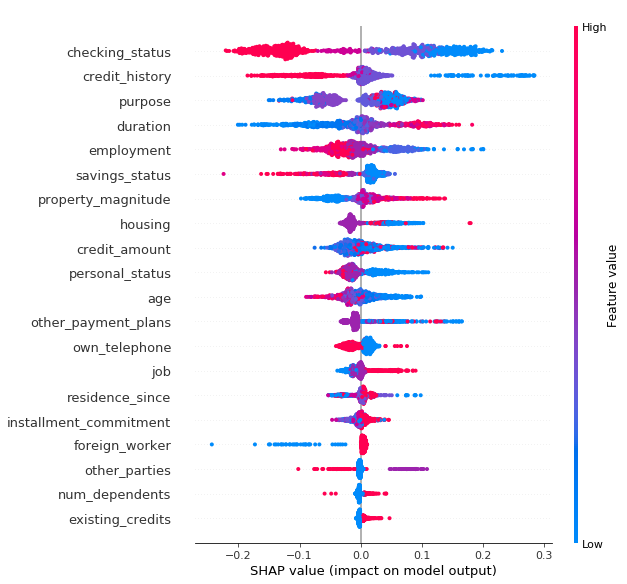

shap3

The figure above shows a plot of all the SHAP values for each feature value against the test data used as input. The top feature values are those that have a greater impact on the prediction values. For example, the results of this calculation show that checking_status and credit_history are effective feature values.

Conclusion

I have briefly introduced a small part of the interpretability of machine learning. I believe that research in this field is conducted assuming that people will apply it on the job to some extent. However, naturally, these research results (tools) will not solve all of the various problems you may encounter on the job.
With the SHAP I introduced in this post, we are not trying to "interpret the problem we want to solve," but rather, "interpret the trained model."

An Explainable model is only an approximate model.
It is still up to the engineers and data scientists working in the field to interpret the output of the explainable model and ensure that it is understood and accepted by stakeholders.

It may sound obvious, but I was reminded through writing this post that engineers must be aware at all times of the importance of proper communication based on an understanding of the characteristics and assumptions of tools.

That is all. Thank you for reading my post. The writer for the last day of Merpay Advent Calendar 2019 will be Merpay CTO @sowawa. I hope you will enjoy the Christmas present from @sowawa!