mercariengineering
twitter
twitter

機械学習における解釈性について

Author:
YuhiK8
 , 
機械学習における解釈性について

こんにちは。Merpay Advent Calendar 2019 の24日目は、メルペイ Machine Learning チームの @yuhi が機械学習における解釈性についてお送りします。

目次

機械学習における解釈性とは

深層学習をはじめとする機械学習分野の発展に伴って、これまでにないユニークなサービスが開発され、また多くの業界において業務が効率化、高度化されつつあります。メルペイでも機械学習を用いて、与信モデルや不正検知などのサービス開発を行っております。

しかし、一般に機械学習はブラックボックスと言われているように、複雑な仮説集合をもつモデルを用いた場合には、なぜその結果となったのか理解できないことが少なくありません。そのため、機械学習の学習、推論結果を人間が容易に解釈できるようにする研究が盛んに行われています[1] 。

解釈性の定義について、明確な定義は存在しないようですが、以下を引用します[2]；

the degree to which
an observer can understand the cause of a decision.

観測者が（機械による）判断の要因を理解できる度合いです。得られたモデルによる推論結果を人間が容易に理解できるような、解釈性が高いということが望ましいのです。

なぜ解釈性が必要なのか

例えば、高い解釈性が必要な理由として以下のような点が考えられます：

  1. サービスを提供する事業者としての説明責任
  2. 推論結果に対する社内外の関係者の理解
  3. モデルのデバッグ、精度改善

1. サービスを提供する事業者としての説明責任

すべての機械学習システムにおいてその説明責任が課されるとは限りません。機械学習を適用しようとしている領域に依存します。総務省により策定されたAI開発ガイドライン案[3]によると；

②透明性の原則——-
開発者は、ＡＩシステムの入出力の検証可能性及び判断結果の説明可能性に留意する。

本原則の対象となるＡＩシステムとしては、利用者及び第三者の生命、身体、自由、プライバシー、財産などに影響を及ぼす可能性のあるＡＩシステムが想定される。

医療や金融、自動運転領域などの、機械学習による推論結果が重大な結果を及ぼす可能性のある領域においては、予測精度だけではなく、解釈性が要求されることは想像に難くありません。むしろ、パフォーマンスを犠牲にしてでも解釈可能なモデルがしばしば用いられています。

2. 推論結果に対する社内外の関係者の理解

機械学習を用いたプロダクト開発やモデリングを担当されている方には特に理解いただけると思いますが、多くのケースにおいて評価指標（e.g. RMSE, AUC）の説明のみで結果を納得してもらうことは難しいです。その背景には様々な理由が考えられますが、予期しない事象に対する好奇心や、発生した事象に対する意味の追求、などといった人間の根源にある性質に関連すると述べられています [4]。

実際、私の過去の経験にも当てはまりますが、学習や推論結果に対するステークホルダーの「なぜ」に答えてあげることで彼らの納得感が得られて、チームとしてビジネスをより前進することができると思います。

3. モデルのデバッグ、精度改善

こちらは開発者視点ですが、モデリング時のデバッグや予測精度改善は非常に重要です。リーケージとなるような説明変数が使われていないかチェックや、説明変数の選択、精度改善のためのエラー分析など、一連のプロセスの中でモデル開発者を力強くサポートし、次のアクションを決めるための情報を提供してくれます。

どのようなアプローチがあるのか

それでは解釈性を提供するアプローチとしてどのようなものがあるのでしょうか。その分類の観点としては様々あるようですが [5]、ここでは記事 [1] を参考にします。

  • 大域的な説明を与えるアプローチ；どの特徴量が重要か、あるいは支配的なのかを知りたい
    • GLM（一般化線形回帰モデル）
    • 決定木
    • Feature Importance
    • Partial Dependence
    • 感応度分析　など
  • 局所的な説明を与えるアプローチ；ある入力対して各特徴量がどのように予測に寄与しているかを知りたい
    • LIME (Local Interpretable Model-agnostic Explanations)[6]
    • SHAP (SHapley Additive exPlanations)[7]　など

本エントリでは、すでにご存知の方もいらっしゃるかもしれませんが、改めてSHAPについて紹介したいと思います。その他手法ついては非常にわかりやすい情報があるので、そちらをご参照いただければと思います[1][8]。

SHAPについて

ここからはSHAPの論文 [7] を中心に紹介していきたいと思います。

しばらく細かな話が続くので、SHAPのツールとしての使用感に興味がある方は「SHAPの実装について」まで進んでいただければと思います。

サマリ

  • LIMEやDeepLIFT、Layer-Wise Relevance Propagation などの解釈性を与える手法は、Additive Feature Attribution Methods として一般化可能。
    • あるデータ点に対して説明可能な近似モデルを構築して貢献度を計算。
  • Additive Feature Attribution Methods は、協力ゲーム理論で用いられる Shapley values と同義。
  • Shapely values は協力ゲームにおける各プレイヤーの貢献度の期待値のこと。ここで各プレイヤーは特徴量と対応（すなわち各特徴量の貢献度を表現していることに対応）。

基本的なアイディア

Additive Feature Attribution Methods では、あるデータ点に関して、学習の結果得られた関数 \(f\) を近似するような関数 \(g\) を求めます。このとき \(g\) について、線形モデルや決定木などの解釈可能な仮説集合を選択することで、あるデータ点の予測結果を解釈できるようにします。

問題設定

入力空間を \(\mathcal X\) 、もとの仮説集合を \(\mathcal H\) とします。\(\mathcal H\) は Gradient Boosting Decision Tree や、Support Vector Machine、Neural Network などユーザが自由にモデルを指定可能です。あるデータ点 \(x \in \mathcal X\) に関して、関数 \(f\in \mathcal H\) を近似するような関数 \(g \in \mathcal G\) を求めます（以後、説明可能モデルと呼びます）。説明可能モデルは、

\(\displaystyle{\mathcal G := \Big\{g:z' \to \phi_0 + \sum_{i=1}^{M}\phi_iz'_i \mid z' \in \{0,1\}^M,\,\phi_0 \in \mathbb R, \phi_i \in \mathbb R\Big\}}\)

のような仮説集合で、この仮説集合の中で \(z' \approx x'\) のときに \(g(z') \approx f\big(h_x(z')\big)\) となるように関数 \(g\) を求めます。ここで、
注目するデータ点 \(x \in \mathcal X\) を単純化したデータ点を \(x' \in \{0,1\}^M\) とします。
単純化したデータ点の空間において、\(0\) は"特徴量が存在しない"、\(1\) は "特徴量が存在する"、に対応しています。
さらに写像 \(h_x : \{0,1\}^M \mapsto \mathcal X\) によって注目するデータ点 \(x \in \mathcal X\) を復元 \(x = h_x(x')\) できることを仮定します。

また、定義から明らかですが、\(\mathcal G\) は線形回帰モデルの集合となっています。

説明可能モデルに対して満たしてほしい性質

次に示す、説明可能モデル \(\mathcal G\) に対して満たしてほしい3つの性質を定めると、その3つの性質を満たすような \(\phi_i\) は次のような形式で一意に定まります。よって、\(g\) が一意に決まります。

\(\displaystyle{\mathcal \phi_i(f, x ) = \sum_{z' \subseteq \ x'}\frac {|z'|!\big(M - |z'| -1\big)!} {M!} \big[f_x(z') - f_x(z_{\setminus i}')\big].}\)

ただし、
\(|z'|\) は \(z'\) ベクトルの非ゼロ要素数、\(z' \subseteq x'\) は \(x'\) の非ゼロ要素の部分集合の元すべて、 \(\ f_x(z') := f_x(h_x(z')) = \mathbb E [ f(z) | z_S ]\)、\(S = \{ i \mid z'_i \neq 0 \}\) を表しています。

なお，この \(\phi_i\) は協力ゲーム理論における Shapley values として知られており、特徴量 \(i\) の貢献度を意味します。

  1. (Local accuracy)

\(\displaystyle{f(x) = g(x')}.\)

これは、\(x = h_x(x')\) とき、すなわち注目するデータ点 \(x \in \mathcal X\) と対応する単純化したデータ点 \(x' \in \{ 0,1 \}^M\) を入力データとして用いたとき、もとのモデルの仮説 \(f \in \mathcal H\) と説明可能モデルの仮説 \(g\in \mathcal G\) の予測値が一致していてほしい、という気持ちを表しています。

  1. (Missingness)

\(\displaystyle{x'_i = 0 \implies \phi_i = 0.}\)

これは、\(x_i'\) が情報欠損しているときは常に貢献度がゼロ、つまり \(\phi_i = 0\) であってほしいという性質です。
実際上は \(x_i\) がデータセット全体で定数値をとる（すなわち無情報）ときに \(x_i'=0\) となるようです(本論文の著者が言及しています。)。

  1. (Consistency)

\(\ f_x(z') := f_x(h_x(z'))\) 、\(z_{\setminus i}'\) は \(j\) 番目の要素がゼロ、すなわち \(z_i' = 0\) を表すこととします。このとき、あるデータ点 \(x \in \mathcal X\) に関して、

\(\forall f, f' \in \mathcal H \space s.t. \space \forall z' \in \{0,1\}^M, \ f'_x(z') - f'_x(z_{\setminus i}') \geq f_x(z') - f_x(z_{\setminus i}'),\ \phi_i(f', x) \geq \phi_i(f, x).\)

これは、特徴量 \(i\) の影響度がより大きい仮説 \(f'\) において、その特徴量 \(i\) の貢献度（Shapley values）もより大きくあってほしい気持ちです。

説明可能モデルを求める

注目するデータ点 \(x \in \mathcal X\) に関して、以下のような問題を考えます(この問題をテストデータセットの件数分解くことになります)。

\(\displaystyle{ \min_ {g \in \mathcal G} \ L(f,g,\pi_{x'}) + \Omega(g). }\)

ただし、

\( \begin{aligned} \Omega(g) &= 0, \\ \pi_{x'}(z') &= \frac {(M-1)} {\tbinom{M}{|z'|}|z'|(M-|z'|)}, \\ L(f,g,\pi_{x'}) &= \sum_{z' \in Z} [f(h_x(z')) - g(z')]^2 \pi_{x'}(z') \end{aligned}\)

とします。

最適化のアルゴリズムは LIME [6] で提案されているものがベースになっています([7] ではLIMEより効率的なサンプリングアルゴリズムが提案されています)。詳細は省略しますが、注目しているデータ点 \(x \in \mathcal X\) 近傍でデータをサンプリングして、それをカーネル関数 \(\pi_x\) によって重みづけして目的関数を評価します。\(\Omega(g), \pi_{x'}({z'}), L(f, g, \pi_x)\) を上述のように定めると実は "説明可能モデルに対して満たしてほしい性質" を満たすため（証明は [7] 参照）、LIMEのアルゴリズムで SHAP values (つまり Shapley values) を計算していることになります。

SHAPの実装について

SHAPは、論文の著者が実装を公開しており、そのツールとしての完成度の高さが特徴です。
現在 PythonのAPIが公開されているため、以後特に宣言なくPythonを用いることとします。
https://github.com/slundberg/shap

オープンなデータセットを用いて簡単にモデリングしつつ、どのようなツールなのかを簡単に紹介したいと思います。
https://www.openml.org/d/40514

問題設定としては、個人の信用リスク（デフォルトしやすさ）の推定です。目的変数は good/bad の2値、説明変数は属性情報や過去の債権情報など20個です(データセットに関して、目的変数の意味は特に記述されておりませんでした（どのようにラベル付けしたのかなど）)。モデルは LightGBM を用いました。
なお今回使用されている特徴量は、メルペイで開発されている与信モデルで使用されている特徴量とは異なります。今回はあくまでもSHAPのデモ用途であるという点についてご理解ください。

import pandas as pd
import numpy as np
import io
import requests
import lightgbm as lgb
import shap
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder

# load JS visualization code to notebook
shap.initjs()

cat_cols = ['checking_status', 'credit_history', 'purpose', 'savings_status',
            'employment', 'personal_status', 'other_parties', 
            'property_magnitude','housing', 'job', 'foreign_worker',
            'own_telephone', 'other_payment_plans', 'class']

def label_encoder(df, cols):
    tmp = df.copy()
    le = LabelEncoder()
    for col in cols:
        tmp[col] = le.fit_transform(tmp[col])
    return tmp

def get_data():
    URL = "https://www.openml.org/data/get_csv/4600907/BNG(credit-g).arff"
    r = requests.get(URL)
    all_df = pd.read_csv(io.BytesIO(r.content), sep=",")
    all_df_enc = label_encoder(all_df, cat_cols)
    df = all_df_enc[:50000]
    X, y = df.drop('class', axis=1), (df['class'] == 0)*1
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
    return X_train, X_test[:1000], y_train, y_test[:1000]

X_train, X_test, y_train, y_test = get_data()

model_lgb = lgb.LGBMRegressor()
model_lgb.fit(X_train, y_train, categorical_feature=cat_cols[:-1])

次に SHAP values を計算します。ここではツリー系のモデルに対して高速に SHAP values を計算できるアルゴリズムである Tree SHAP[9]を用いています。なお、SHAPの論文[7]で提案されているアルゴリズムは shap.KernelExplainer クラスと対応しています。

# explain the model's predictions using SHAP values
# (same syntax works for LightGBM, CatBoost, scikit-learn and spark models)
explainer = shap.TreeExplainer(model_lgb)
shap_values = explainer.shap_values(X_test)

SHAPで提供されているメソッドをいくつか紹介したいと思います。

# visualize the first prediction's explanation (use matplotlib=True to avoid Javascript)
shap.force_plot(explainer.expected_value, shap_values[32,:], X_test.iloc[32])

shap1

上図はある予測対象のデータに対して、各特徴量がどのように予測値に対して寄与しているかを可視化しています。赤い特徴量がポジティブシフト（今回は信用リスクが増加する方向）、青い特徴量がネガティブシフト（今回は信用リスクが低下する方向）に寄与しています。この例では、実際のラベルは 1 なのですが、予測された信用リスクが 0.80 程度で、checking_status（当座預金口座の状態）や credit_history（過去の債権情報）などが予測値に大きく寄与しているということがわかります。

explainer.expected_value + shap_values[32,:].sum() # 0.8049431508030044
model_lgb.predict(X_test)[32] # 0.8049431508030043

1行目では得られた説明可能モデル \(g(z') = \phi_0 + \sum_{i=1}^{M}\phi_iz_i'\) の出力値を計算しています。explainer.expected_valueが \(\phi_0\) と対応しています。2行目は学習したモデルの出力値です。それぞれほぼ同じ出力値が得られていることがわかりますね。

# visualize the training set predictions
shap.force_plot(explainer.expected_value, shap_values, X_test)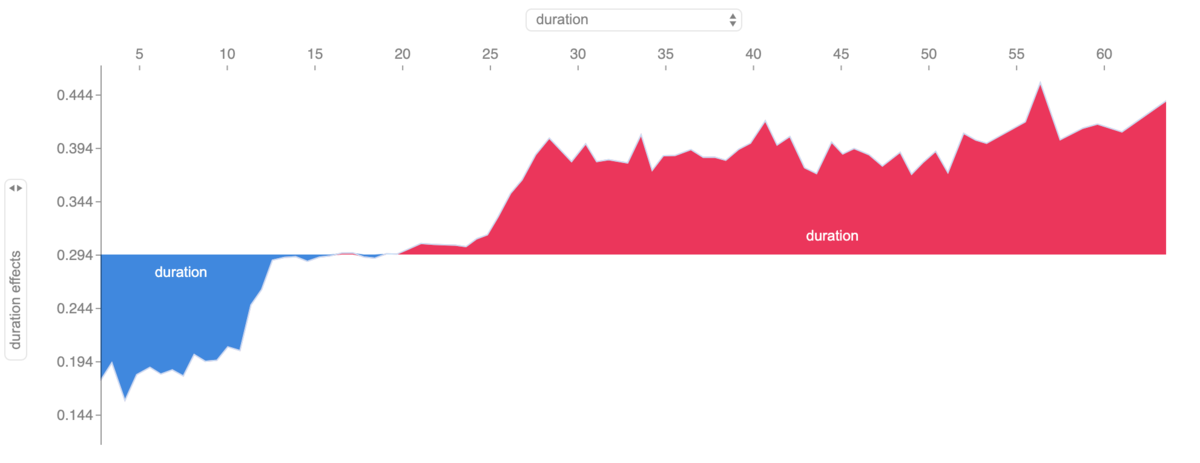

shap2

上図は単一の特徴量が予測値にどのような影響を与えるを可視化したものです。特徴量の値の変化に対して予測値がどう変化するかを確認することができます。この機能はインタラクティブで、2軸を自由に変更することができます。この図では、延滞月数が長い人（横軸の右方向）は信用リスクが大きくなる傾向があることがわかります。

# summarize the effects of all the features
shap.summary_plot(shap_values, X_test)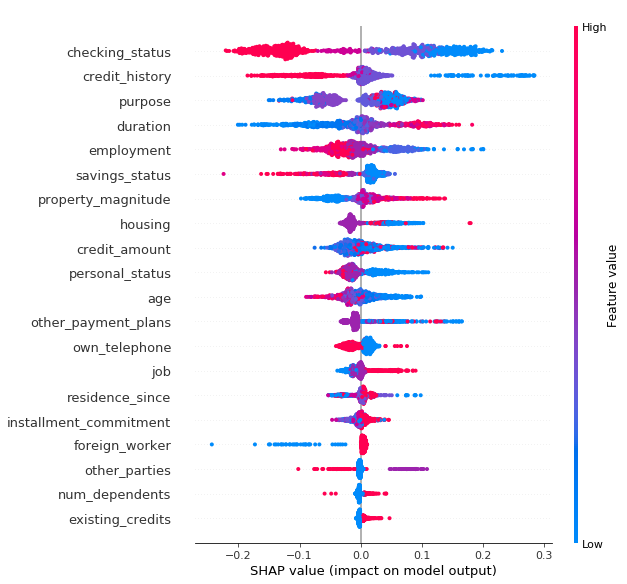

shap3

上図は入力に使用したテストデータに対して、特徴量毎のSHAP values をすべてプロットしたものです。上位の特徴量は予測値に対してより大きな影響を与えているそれとなっています。今回の結果では、checking_status や credit_history が有効な特徴量であることがわかります。

最後に

機械学習の解釈性について簡単にほんの一部だけですが紹介いたしました。この分野の研究は実際にそれが現場で使われることある程度想定して進められていると思いますが、当然それら研究成果（ツール）によって現場の様々な問題が万事解決というわけではないと思います。
今回紹介したSHAPについても、"解きたい問題の解釈"をしているわけではなく、あくまで"学習済みモデルの解釈"をしようとしているのです。

  • 説明可能モデルはあくまで近似モデルである
  • 説明可能モデルの出力をどのように解釈し、ステークホルダーの理解や納得が得られるかどうかは、依然として現場のエンジニアやデータサイエンティストに依存しているのは変わらない

当たり前といえば当たり前ですが、ツールの特性や仮定を理解した上で、適切なコミュニケーションを取ることが重要である点はエンジニアとして常に意識しないといけない点であると、本エントリの執筆を通じて改めて感じました。

以上となります。最後までお付き合いいただきありがとうございました。Merpay Advent Calendar 2019 の最終日はメルペイCTO @sowawa さんです。@sowawa さんからのクリスマスプレゼントをお楽しみに！

References
  • X
  • Facebook
  • linkedin
  • このエントリーをはてなブックマークに追加

Related article